The Problems of Spacetime and Multidimensional Space

Imagine a pendulum swing like the one in the animation below and think about its resulting trajectory in space and time. In which of the points on this curved trajectory has the pendulum been during the swing? At which points in time has the pendulum been on the trajectory during its swing?

Continuity of space and time

Todays intuition indicates that space and time are continuous. But this has not always been the popular opinion. Continuity needs the concepts of infinity and infinitesimal units of space and time, which, to be honest, are not always intuitive.

Zeno’s Paradox: The Dichotomy

Suppose Atalanta wishes to walk to the end of a path, say she is headed to her next seminar. Before she can get there, she must get halfway there. But before she can get halfway there, she must get a quarter of the way there. Before traveling a quarter, she must travel one-eighth; before an eighth, one-sixteenth; and so on.

This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can be neither completed nor begun, and so all motion must be an illusion. So much for taking “the first step”.

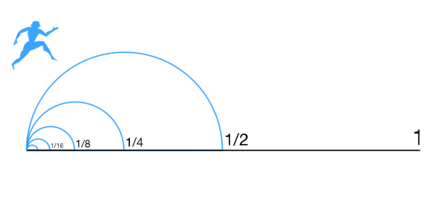
Fig. 18 Zeno’s Paradox of Dichotomy of continuous Space, from Wikipedia.

You could turn the dichotomy paradox around and imagine staying in front of a wall. Then it should be easy to take a step forward that halves the distance between you and the wall. Take a second step that halves that distance again between you and the wall. Try it again. And again. If you continue halving the distance, will you ever bump your head against the wall?

Zeno’s Paradox: Achilles and the Tortoise

Quote

“In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.” - Zeno of Elea, as recounted by Aristotle

In this paradox, Achilles is in a footrace with the tortoise (see Fig. 19). Achilles allows the tortoise a head start of 100 meters, for example. Suppose that each racer starts running at some constant speed, one faster than the other. After some finite time, Achilles will have run 100 meters, bringing him to the tortoise’s starting point. During this time, the tortoise has run a much shorter distance, say 2 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles arrives somewhere the tortoise has been, he still has some distance to go before he can even reach the tortoise.

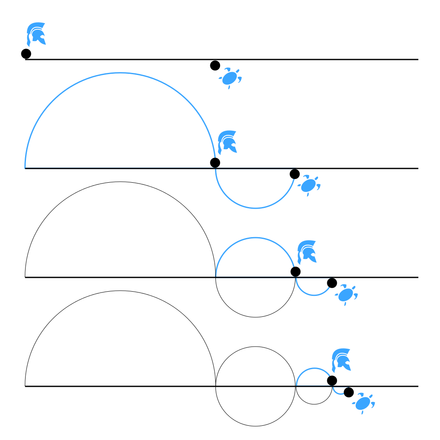
Fig. 19 Zeno’s Paradox of Achilles and the Tortoise, from Wikipedia.

Zeno’s Paradox: The Arrow

In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (duration-less) instant of time, the arrow is neither moving to where it is, nor to where it is not. It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.

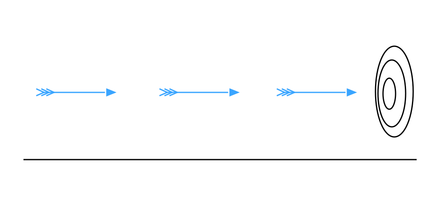
Fig. 20 Zeno’s Paradox of the Arrow and instantaneous motion, from Wikipedia.

Solution: Calculus, yes really

A breakthrough in the study of continuous change was the development of calculus in 17th-century Europe by Isaac Newton and Gottfried Wilhelm Leibniz, but elements of it appeared in ancient Greece, in China and in the Middle East. Using integration, differentiation, infinite series and limits, Zeno’s paradoxes can be explained. For example, the resolution of the paradox of Achilles and the Tortoise is that, although the series have an infinite number of terms, it has a finite sum, which gives the time necessary for Achilles to catch up with the tortoise. This is the difference between convergent and divergent infinite series.

Take Home Message

Without getting into too much detail about the mathematical foundations of calculus, or the physics of the curvature of spacetime in the general theory of relativity, or the Planck scale of quantum mechanics, what can you make out of this discussion? What does it mean for you to move and behave in spacetime?

Try to write a short statement about behavior in spacetime with max. 150 words:

“If you consider Zeno’s Arrow-Paradox, the gist of it is that movement is an illusion, because watching movement at a single point in time results in a still image. I would consider this conclusion to be hasty. Movement or behavior as such is dependent on space. Without space there would be no reference as to where something moves or in which direction. Time, however, can tell us how fast a movement is, it can tell us when a behavior started and ended. Behavior is the “When” relative to the “Where” and the “Where” relative to the When”. Taken together, time and space are the “What” that describes behavior. Without either of these you cannot define behavior or movement. Because taking time or space out of the equation makes it unsolvable. The Zeno’s illusion is that the equation does not exist. However, it does. It is the “What” of behavior.”

“What is space? What is time? What is behavior? All of these terms describe theoretical constructs - each of them being continuous in nature - and each of them being hard to define. To my knowledge, there is no conclusive definition of the term “behavior” and probably the same is true for the concepts of time and space.
For practical purposes in the field of computational ethology, I would define “behavior in spacetime” as the total sum of all the (internal & external) responses to (internal or external) stimulation of an animal in “time” and “space” as measured in standard metrical time- / length scales. However, with respect to Zeno’s Paradox, this approach can only be an approximation to what “behavior in space and time” is, but for the purpose of measuring and studying animal behavior with our current understanding, I believe it to be sufficient.”

Measuring in Multidimensional Space

Given the methods and techniques from Computational Ethology learned in the previous lectures, it seems we have improved vastly our methods of observation using high resolution video imaging. But are video recordings really that good?

Reducing a given scene to a two dimensional plane on a video frame looses valuable information essential for behavioral analysis. Given specific visual cues, humans have no problem whatsoever reconstructing three dimensional objects and inferring the missing or occluded parts. Computational models are not quite there yet, although promising approaches for 2D-to-3D lifting exist (see Bonus II below).

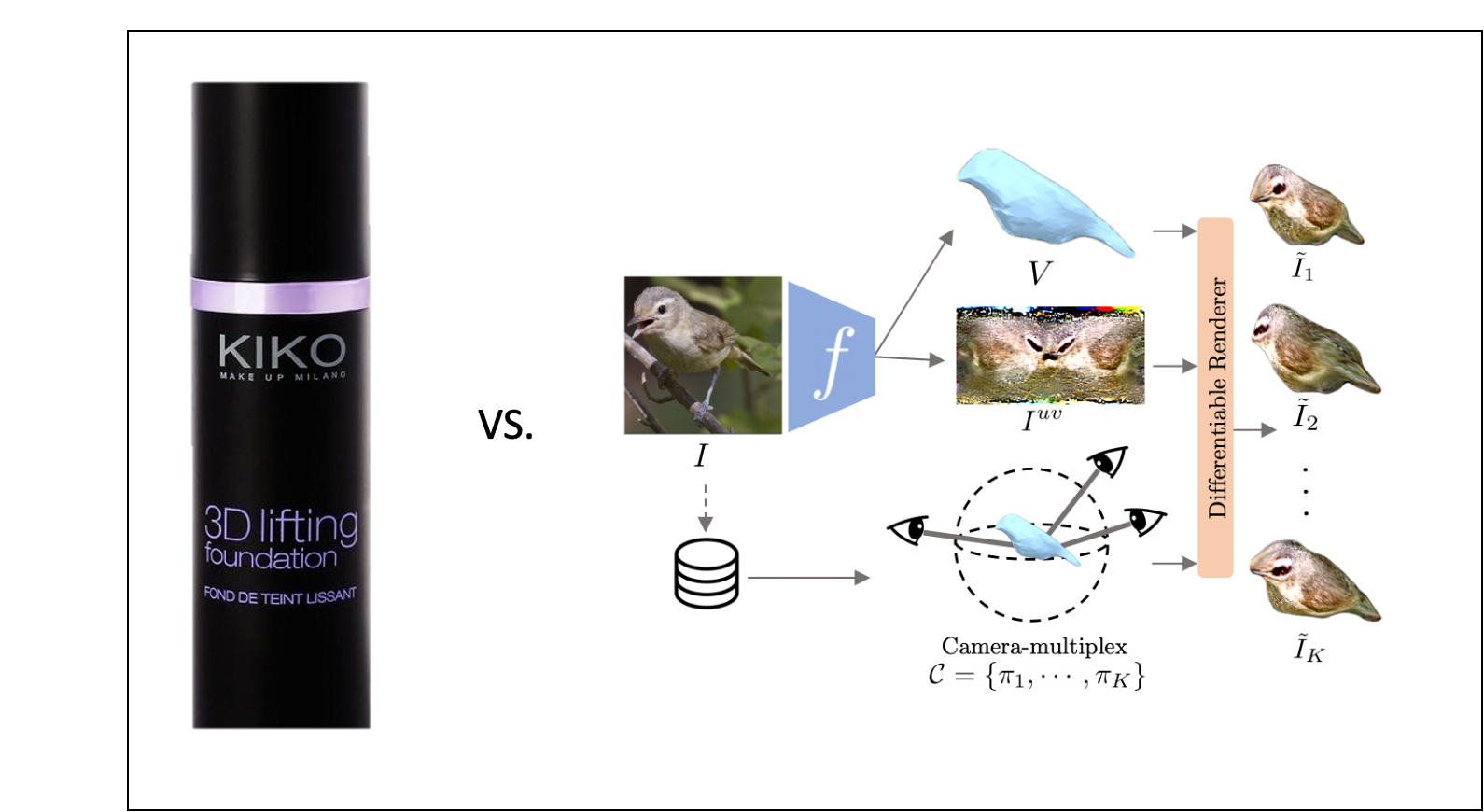
Fig. 21 2D to 3D lifting techniques.

Until then, we are stuck with the problem of reconstructing 3D objects from 2D image representations by multi-view synchronized recording and camera triangulation. Different methods have proved to be successful in computational ethology (see Dunn et al., 2021; Karashchuk et al., 2021). But many question remain. How many cameras are needed? Where to position the different cameras?

Temporal Synchronization

Literature

Dunn, T. W. (2021). Geometric deep learning enables 3D kinematic profiling across species and environments. Nature Methods, 18, 17. https://doi.org/10.1038/s41592-021-01106-6

Karashchuk, P., Rupp, K. L., Dickinson, E. S., Walling-Bell, S., Sanders, E., Azim, E., Brunton, B. W., & Tuthill, J. C. (2021). Anipose: A toolkit for robust markerless 3D pose estimation. Cell Reports, 36(13), 109730. https://doi.org/10.1016/j.celrep.2021.109730

Bonus: Jesse Marshall (Harvard University)

Exiting flatland: measuring, modeling, and synthesizing animal behavior in 3D

Bonus II: Angjoo Kanazawa (Berkley University)

TUM AI Lecture Series - Perceiving Humans in the 3D World